Smallest Subtree with all the Deepest Nodes
题目
Given a binary tree rooted at root, the depth of each node is the shortest distance to the root. A node is deepest if it has the largest depth possible among any node in the entire tree. The subtree of a node is that node, plus the set of all descendants of that node. Return the node with the largest depth such that it contains all the deepest nodes in its subtree.
题目很拗口,主要的意思是找到一棵二叉树中包含所有最底层节点的最小子树。
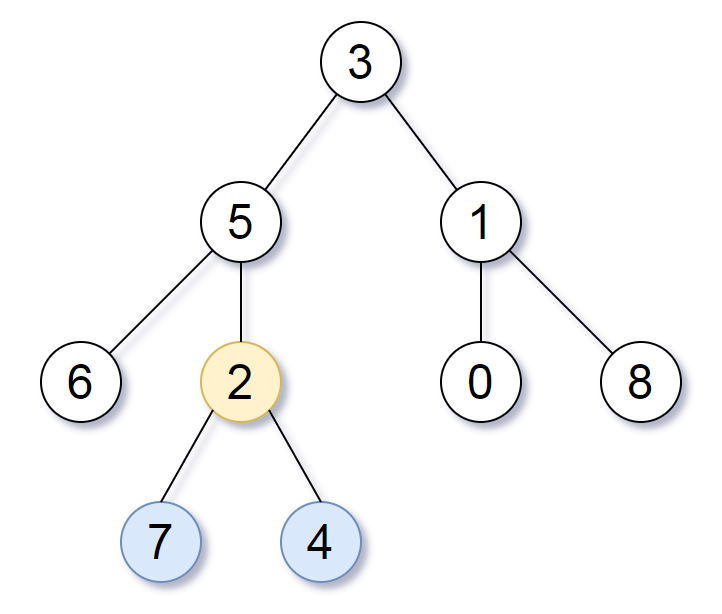
如上图,二叉树高度为4,且深度为4的节点有两个:7,4。包含节点7,4的最小子树就是2,7,4。将其输出即可。
分析
对于算法题的求解,通常有一种取巧的突破方式:首先我们假设得到了答案,再根据答案的描述去反推其性质,遇到特别的性质,只要能够证明该性质是答案的充要条件,即可将问题转化为另一个更简单的问题。
令depth(node) = 该节点的深度, maxDepth(node) = 该节点树中深度最大节点的深度值。假设x为其他任意节点,我们要找的根节点满足以下两点要求:
- 因为答案节点必须包含所有最底层节点,所以maxDepth(node) == maxDepth(root) >= maxDepth(x)
- 答案节点是包含所有最底层节点的最小子树,即答案节点的深度是所有最大深度等于maxDepth(root)的节点中最深的,数学语言描述:当maxDepth(node) == maxDepth(x)时, depth(node) < depth(x); 这样的节点有且仅有一个,找到满足以上条件的节点即答案。 因此,我们只要求出每一个节点的maxDepth与depth两个值,再进行比较即可得到答案。因此,我们只需要对树做一次遍历,在遍历时记录满足以上条件的极值即可。算法的时间复杂度为O(N),空间复杂度为O(N),但是有递归栈的开销。
优化:通常可找到答案节点的某些必要不充分条件减少程序运行时间。 假设我们获取到了答案,子树的根节点为sroot。我们可以发现一个有趣的性质:sroot的左子树深度必然等于sroot的右子树深度。 证明:假设sroot是二叉树中包含所有最底层节点的最小子树,其左子树根节点为scl,右子树根节点为scr。且scl的深度比scr的深度大1. 证:令scl子树中深度最深的子节点在整棵树中深度为h 由于scr子树深度比scl的深度小1,因此scr子树中深度最深子节点深度为h-1 由于sroot为包含所有最底层节点的最小子树,所以整棵树深度最深节点的深度为h 由于scr子树中深度最深节点的深度为h-1,因此scr子树不包含任何深度为h的节点 因此scl应为root树种包含所有最深节点的子树,与假设冲突 同理可证scr > srl的情况 结论得证。
代码
class Solution {
private TreeNode result = null;
private int resultMaxDepth = 0;
private int resultDepth = 0;
public TreeNode subtreeWithAllDeepest(TreeNode root) {
maxDepth(root, 0);
return result;
}
public int maxDepth(TreeNode root, int depth) {
if (root == null) {
return depth;
}
int maxLeftDepth = maxDepth(root.left, depth + 1);
int maxRightDepth = maxDepth(root.right, depth + 1);
if (maxLeftDepth == maxRightDepth) {
if (maxLeftDepth > resultMaxDepth) {
resultMaxDepth = maxLeftDepth;
resultDepth = depth;
result = root;
} else if (maxLeftDepth == resultMaxDepth) {
if (depth < resultDepth) {
resultMaxDepth = maxLeftDepth;
resultDepth = depth;
result = root;
}
}
}
return maxLeftDepth > maxRightDepth ? maxLeftDepth : maxRightDepth;
}
}
结果如下: Runtime: 2 ms, faster than 100.00% of Java online submissions for Smallest Subtree with all the Deepest Nodes. Memory Usage: 38 MB, less than 8.11% of Java online submissions for Smallest Subtree with all the Deepest Nodes.